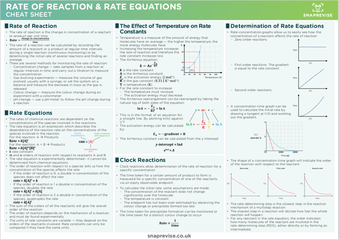
Rate of Reaction
- The rate of reaction is the change in concentration of a reactant or product per unit time.
- The rate of a reaction can be calculated by recording the amount of a reactant or a product at regular time intervals during a single reaction (continuous monitoring) or by determining the initial rate of several reactions and finding an average.
- There are several methods for monitoring the rate of reaction:
- Concentration change- take samples from a reaction at regular intervals in time and carry out a titration to measure the concentration
- Gas evolving experiments- measure the volume of gas evolved, usually with a syringe, or set the system on a balance and measure the decrease in mass as the gas is released
- Colour change- measure the colour change during an experiment with a colorimeter
- pH change- use a pH meter to follow the pH change during a reaction
Rate Equations
- The rates of chemical reactions are dependent on the concentrations of the species involved in the reactions.
- The rate equation is an expression which describes the dependence of the reaction rate on the concentrations of the species involved in the reaction.
Rate = k[A]^x
For the reaction: A + B → Products
Rate = k[A]^m[B]^n
k rate constant
m and n orders of reaction with respect to reactants A and B
For the reaction: A + B → Products
Rate = k[A]^m[B]^n
k rate constant
m and n orders of reaction with respect to reactants A and B
- The rate equation is experimentally determined– it cannot be determined from chemical equations.
- The order of reaction with respect to a species tells us how the concentration of the species affects the rate
- If the order of reaction is 0, a double in concentration of the species does not affect the rate rate = k[A]^0 = k
- If the order of reaction is 1 a double in concentration of the species, doubles the rate rate = k[A]^1 = k[A]
- If the order of reaction is 2 a double in concentration of the species, quadruples the rate rate = k[A]^2
- The sum of the orders of all the reactants will give the overall order of the reaction
- The order of reaction depends on the mechanism of a reaction and must be found experimentally
- The units of rate constants are variable- they depend on the orders of the reactants involved. Rate constants can only be compared if they have the same units.
The Effect of Temperature on Rate Constants
- Temperature is a measure of the amount of energy that molecules have on average – the higher the temperature, the more energy molecules have.
- Increasing the temperature increases the rate of reaction and therefore the rate constant increases too
- The Arrhenius equation:
k is the rate constant
A is the Arrhenius constant
Ea is the activation energy (Jmol^-1)
R is the gas constant (8.31 J K^-1mol^-1)
T is temperature (K)
A is the Arrhenius constant
Ea is the activation energy (Jmol^-1)
R is the gas constant (8.31 J K^-1mol^-1)
T is temperature (K)
- For the rate constant to increase:
- The temperature must increase
- The activation energy must decrease
- The Arrhenius rearrangement can be rearranged by taking the natural log of both sides of the equation:
- This is in the format of an equation for a straight line. By plotting ln(k) against 1/T
- The activation energy can be calculated by:
- The Arrhenius constant can be calculated from the y intercept
Clock Reactions
- Clock reactions allow determination of the rate of reaction for a specific concentration
- The time taken for a certain amount of product to form is measured for a specific concentration of one of the reactants via an easily observable endpoint.
- To calculate the initial rate, some assumptions are made:
- The concentration of the reactant does not change significantly over the timescale
- The temperature is constant
- The endpoint has not been over-estimated by observing the colour change or precipitate formed too late
- The time taken for precipitate formation can be monitored or the time taken for a distinct colour change to occur
Determination of Rate Equations
- Rate-concentration graphs allow us to easily see how the concentration of a reactant affects the rate of reaction
- Zero order reactions
- First order reactions. The gradient is equal to the rate constant.
- Second order reactions
- A concentration-time graph can be used to calculate the initial rate by drawing a tangent at t=0 and working out the gradient.
- The shape of a concentration-time graph will indicate the order of the reaction with respect to the reactant
- The rate-determining step is the slowest step in the reaction mechanism of a multistep reaction.
- The slowest step in a reaction will dictate how fast the whole reaction will happen
- For any reactant in the rate equation, the order indicates how many molecules of the reactant are involved in the rate-determining step (RDS), either directly or by forming an intermediate